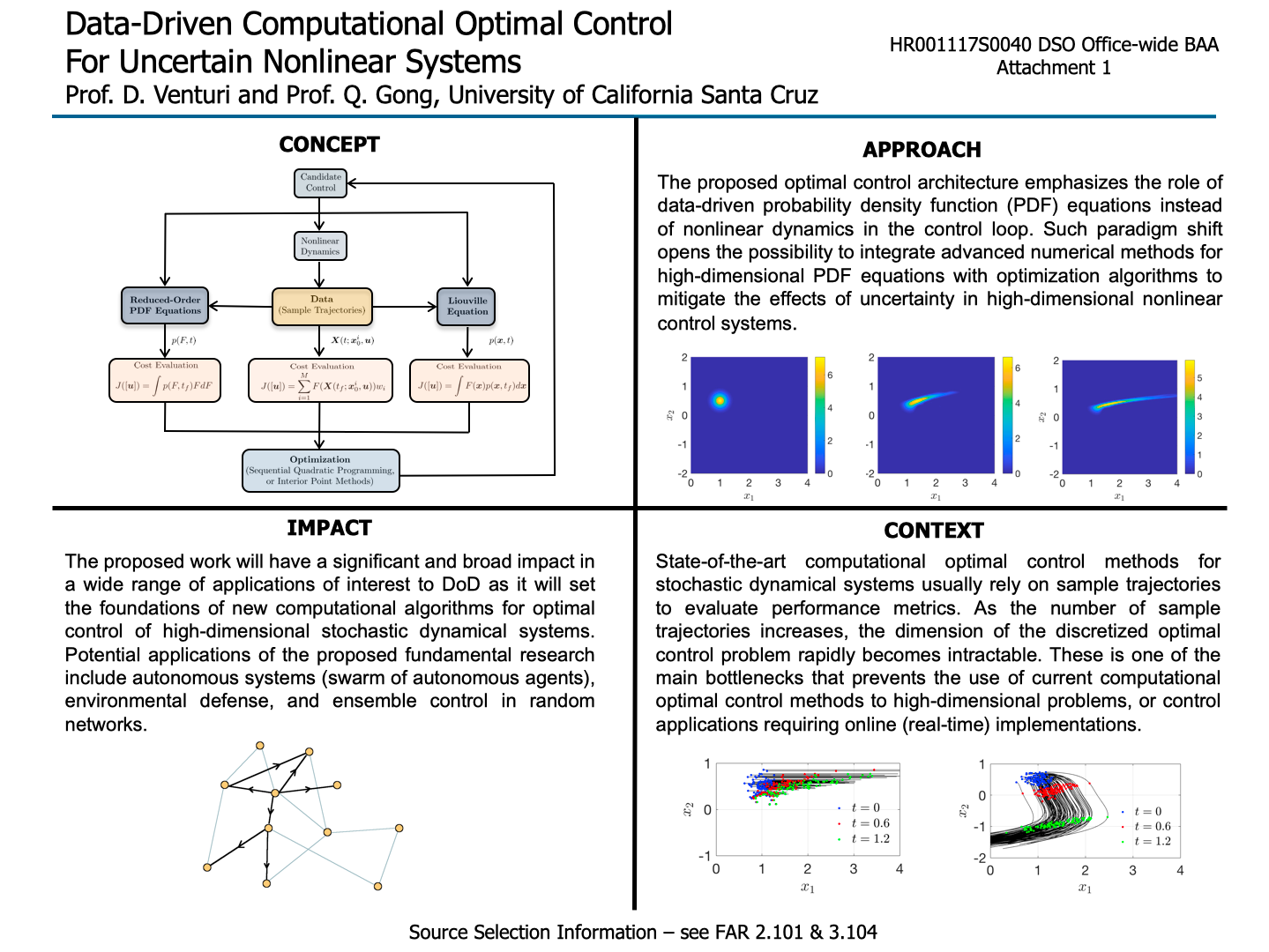
In this proposal, we address a very important research area in computational mathematics, namely the design and synthesis of optimal control strategies for high-dimensional stochastic dynamical systems. Such systems may be classical nonlinear systems evolving from random initial states, or systems driven by random parameters or processes. The first objective is to provide a validated new computational capability for optimal control of stochastic systems which will be achieved at orders of magnitude more efficiently than current methods based on spectral collocation or random sampling. To accomplish this goal, we will develop a new data-driven optimal control framework based on probability density function (PDF) equations. The new framework is built upon high-order numerical tensor methods, with no specific requirements on the structure of the continuous dynamics, cost function, or the type of uncertainties. The 18 months research plan is multidisciplinary and it involves multiple fields such as optimal control, large-scale optimization, and uncertainty quantification. It consists of theoretical and numerical developments, as well as a general software framework that will implement the proposed algorithms. The proposed research work will have a significant and broad impact in a wide range of engineering applications such as autonomous systems, environmental defense, and ensemble control of random networks.